社会インフラとプラットフォーム
（生産道具と記録形式）
道具 形式 実践
21 22 23

道具

１．製図作業の能率化
２．パース（透視図）
３．景観シミュレータの頃(1993-6)

１．製図作業の能率化

近世以前

・和紙に筆で製図
・現場での板図
・尺杖（高さ方向の基準寸法）

1980年代

・製図版→平行定規
・T定規、三角定規→ドラフター
・鉛筆：下描き
・白焼きによるコピー
・納品用製図、記録保存：烏口→ロットリング

CADソフト＋XYプロッター

・民家調査清書用（KAOSYS/N88BASIC)
　ディスプレイに方眼罫を表示し、格子点に柱を指定
　二つの柱の間に柱間装置の記号を選択（壁、引き戸、窓・・）
　１住宅一日の版下清書作業が２時間程度に

・建築確認用の国産CAD
　日本の場合、施工中の設計変更が頻繁であり鉛筆プロッタが中心 （現場で消しゴムで修正できる図面が必要）

２．建築パース（透視図）

・多数の補助線、中間点を製図する時間のかかる作業 ・コンピュータでの処理 　・多数の補助線、中間点を製図する時間のかかる作業
・コンピュータでの処理 射影変換
（X,Y,Z)→(X/Z,Y/Z)
 ワイヤーフレーム→大手設計事務所によるプレゼン

・QUADRA900を用いた、市街地自動生成結果のプレゼン（二本松） （画面の１ピクセル毎に表示すべき色を計算するThink-C プログラム）

３．景観シミュレーション

・SGIによる高速マシン
・GLによるプログラミング
・正確な写真合成への期待（画像視点抽出）
・フル３Ｄの夢／高速描画のための様々な小技
・CALS/ECの萌芽（ID→CAM)
・建設技術評価制度（DEMの精度検定用形式）

形式

４．ネイティブ形式
５．三次元標準形式
６．展開

４．ネイティブ形式

・道具毎に、作業結果を保存する独自形式
・最終製品は紙に記録された在来媒体
（データそのものではない）
・二次元：プロッタ駆動
・三次元：パース描画
・建築の場合、構造、積算、環境（音響）との
連携が課題

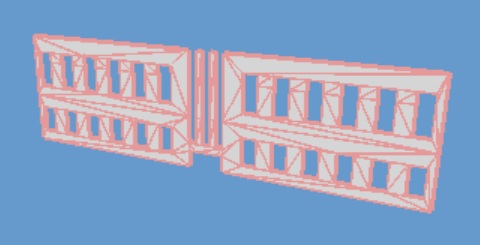
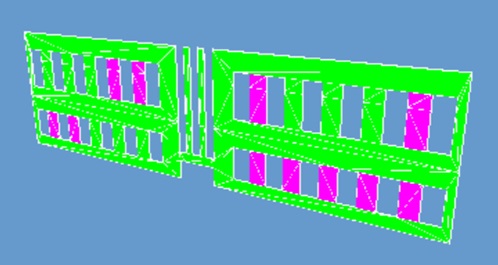
DXF形式は、AutoCADの外部ファイル形式（ネイティブ）であったが、テキスト形式であり マニュアルにフォーマットが解説されていたことから、データ交換に表現使用された。 二次元から三次元に拡張された。 形状は記述できるがマテリアルやテクスチャを表現することはできない。
 ファイルサイズが大きい点が難点であったが、記憶容量の制約がなくなり、 圧縮通信が普及したため、問題とはならなくなっている。

（前略）
10
390.0
20
1332.000244140625
30
99.99994659423828
10
1008.0
20
1330.000366210937
30
2098.0
10
1010.0
20
1332.000366210937
30
2100.0
10
1008.0
20
1330.000244140625
30
101.9999465942382
10
1010.0
20
1332.000244140625
30
99.99994659423828
93
　　 4800
90
　　　　3
90
　　　294
90
　　　305
90
　　　304
90
　　　　3
90
　　　304
90
　　　295
90
　　　294
90
　　　　3
90
　　　295
90
　　　304
90
　　　299
90
　　　 3

SKV形式（略）
SHP形式（略）
総務省の三次元GIS標準化の試み（略）

５．三次元標準形式

・GL, OpenGL 原始的なポリゴン、視点、光源
（アプリケーションから呼び出すライブラリ関数群）
OpenGLは、現在でも広く使用されており、スマホ、タブレット等でも利用可能
グラフィック・アクセラータ(GPU)の併進処理により表示が高速化した
 ・Open Inventor形式
（ファイル形式.iv、基本的な原始立体）
この形式自体は現在「古語」であるが、現在の多くの
ファイル形式がこの形式から発展したものと考えられる

基本形式
ノード名{
　フィールド名　フィールド値
　フィールド名　フィールド値
　　　・・・・
｝

例：
RotationXYZ{
  axis Z
  angle 3.1415
}                                      Z軸の周りに3.1415ラジアン回転する

Cylinder{
  parts  All
  radius 1
  height 2
}                      半径１、高さ２の円柱の全て（上底、下底、側面）を表示

・VRML（ファイル形式、1998.1.27にISO/IEC14772-1として、VRML9.7が標準化）

基本形式
ノード名{
　フィールド名　フィールド値
　フィールド名　[フィールド値, フィールド値、フィールド値、・・・・]
フィールド名 ノード名{フィールド名 フィールド値} 
　　　・・・・
｝

例：
#VRML V2.0 utf8
#LSS sim.exe
#Copyright(C) Ministry of Construction 1993-1996
Group{
　children[
　　DEF BUMI Transform{ #GROUP(unknown) type=0
　　　children[
　　　　Shape{ #FACE
　　　　　appearance Appearance{
　　　　　　material Material{
　　　　　　　diffuseColor 0.34 0.8 0.4
　　　　　　}
　　　　　}
　　　　　geometry IndexedFaceSet{
　　　　　　coord Coordinate{
　　　　　　　point[800 132.326 -800,
　　　　　　　　900 70.9149 -900,
　　　　　　　　800 99.2971 -900,
　　　　　　　　900 91.9956 -800,
　　　　　　　　700 158.539 -800,
　　　　　　　　700 115.522 -900,
　　　　　　　　600 160.248 -800,
　　　　　　　　600 113.279 -900,
　　　　　　　　500 140.381 -800,
　　　　　　　　（中略）
　　　　　　　　300 85.649 -0,
　　　　　　　　200 94.4877 -0,
　　　　　　　　100 95.797 -0,
　　　　　　　　0 83.7789 -0 ]
　　　　　　}
　　　　　　coordIndex[
　　　　　　　0,1,2,-1,
　　　　　　　0,3,1,-1,
　　　　　　　4,2,5,-1,
　　　　　　　4,0,2,-1,
　　　　　　　6,5,7,-1,
　　　　　　　6,4,5,-1,
　　　　　　　8,7,9,-1,
　　　　　　　（中略）
　　　　　　　98,87,88,-1,
　　　　　　　98,97,87,-1,
　　　　　　　99,88,89,-1,
　　　　　　　99,98,88,-1]
　　　　　　normalPerVertex FALSE
　　　　　　ccw FALSE
　　　　　　solid FALSE
　　　　　}
　　　　}
　　　]
　　}
　]
}

以上 頂点座標を羅列しておき、頂点番号を参照する形でポリゴンを定義している。 

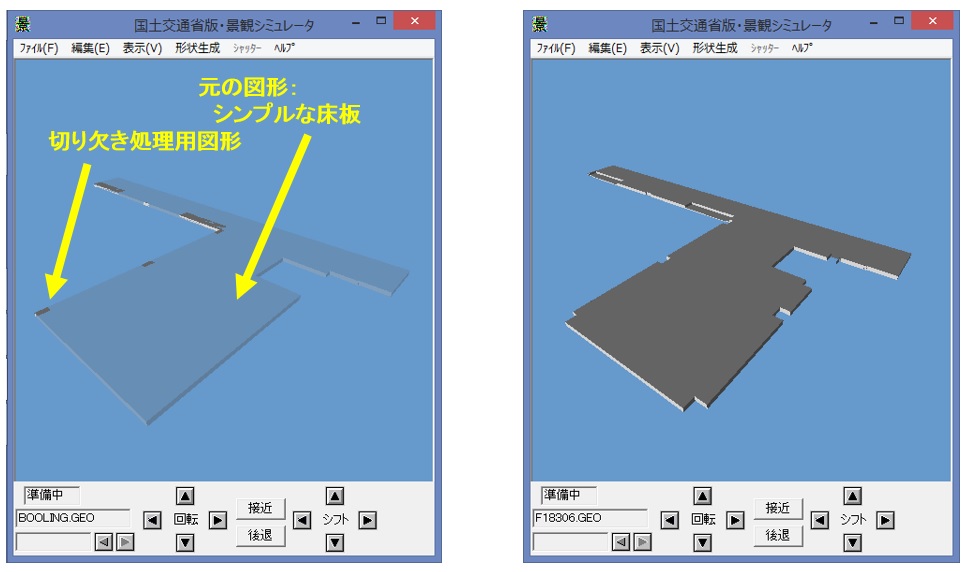
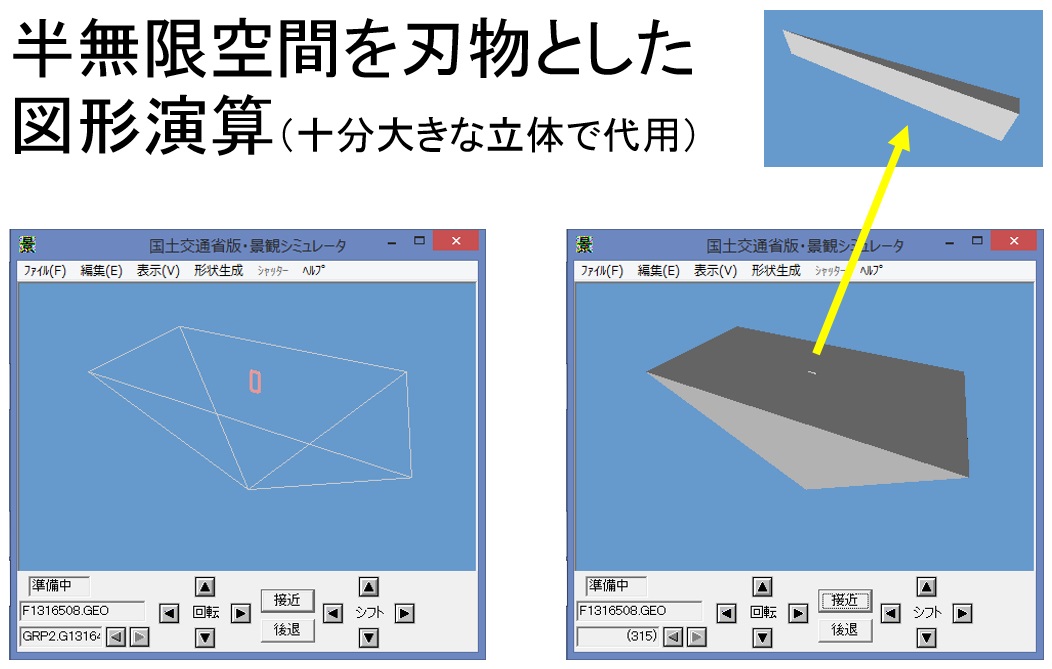
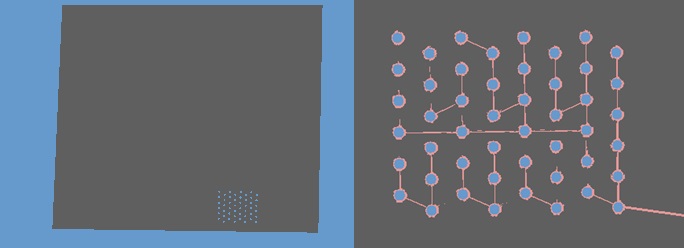
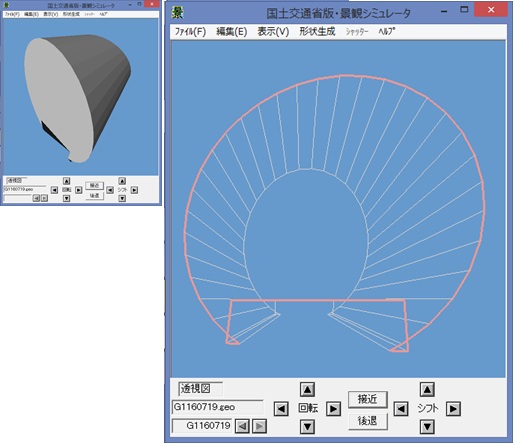
景観シミュレータの外部ファイル形式（LSSG）は、Open Inventor形式をベースに策定されたが、
記法として、C言語ライクな関数形式で表現している。
# (ip ver.2.09) 国土交通省版・景観シミュレータ  2.09
　GRP2 = GROUP();
　CONCAVE(ON);
　V00 = COORD(1,1.4,0);
　C00 = COLOR(0, 0, 1, 1);
　V01 = COORD(0,0,0);
　C01 = COLOR(1, 0, 0, 1);
　V02 = COORD(2,0,0);
　C02 = COLOR(0, 1, 0, 1);
　V03 = COORD(1.106,0.679,0);
　C04 = COLOR(0.2045, 0.3105, 0.485, 1);
　V04 = COORD(1.21,0.33,0);
　C05 = COLOR(0.277143, 0.487143, 0.235714, 1);
　V05 = COORD(0.733,0.306,0);
　C06 = COLOR(0.524214, 0.257214, 0.218571, 1);
　P00 = VERTEX(V00, , , C00, V03);
　P01 = VERTEX(V01, , , C01);
　P02 = VERTEX(V02, , , C02);
　P03 = VERTEX(V03, , , C04, V00);
　P04 = VERTEX(V04, , , C05);
　P05 = VERTEX(V05, , , C06);
　F00 = FACE(P00, P01, P02, P00, P03, P04
　　, P05, P03);
　N08 = NORMAL(0, 0, 1);
　FACE_NORMAL(F00, N08);
　GROUP_FACE(GRP2, F00);

SKV形式（富士通バーチャルモール、略）
SHP形式（Arc Info、GISのデファクト交換形式、略）
総務省の三次元GIS標準化の試み（略）

６．多様な展開

標準化にかかわらずVRML形式は定着せず、その後も様々のデータ形式が目的別に成立した。
各種アプリケーションにおいても主要な入出力フォーマットが選択できるようになっている。
tbl1 tbl1 tbl1 tbl1
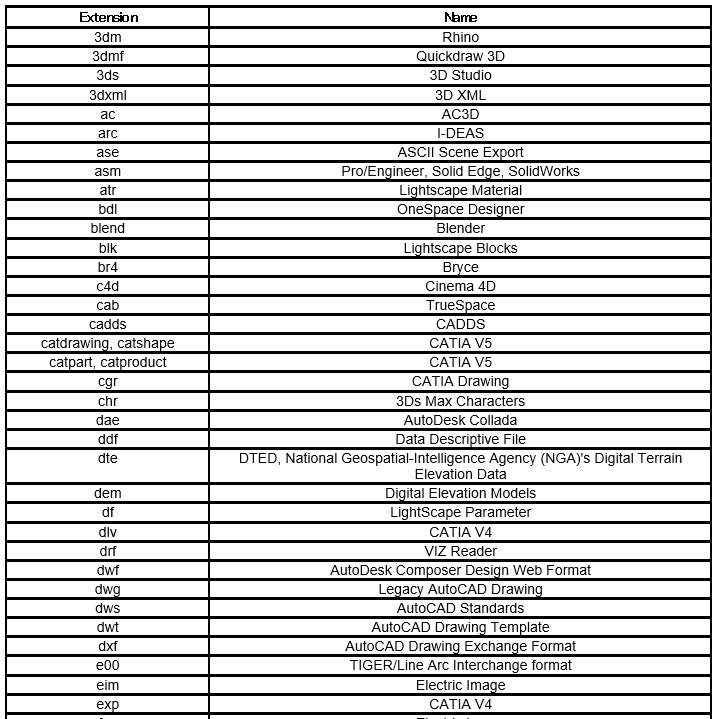
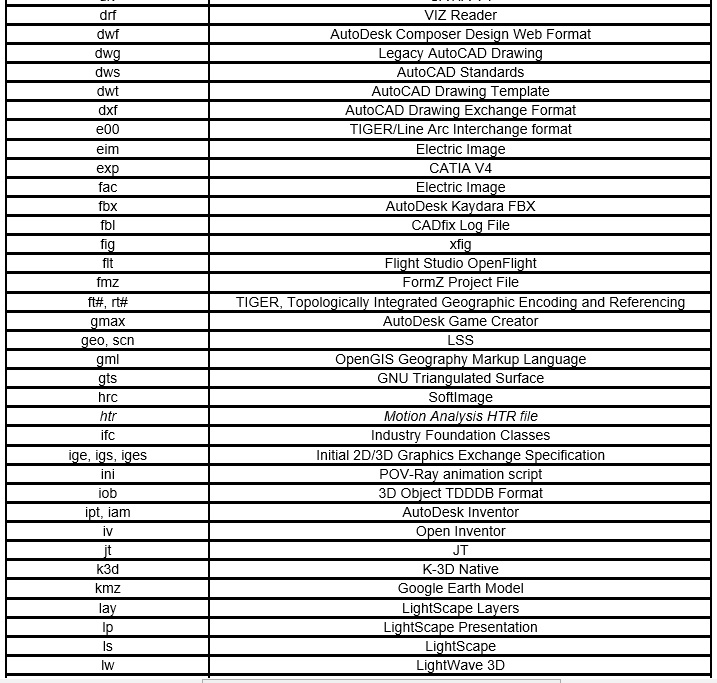
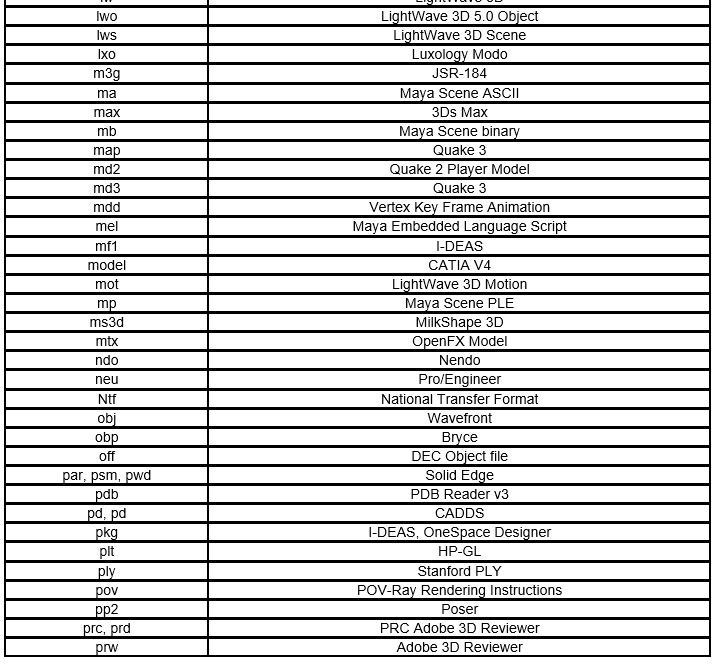
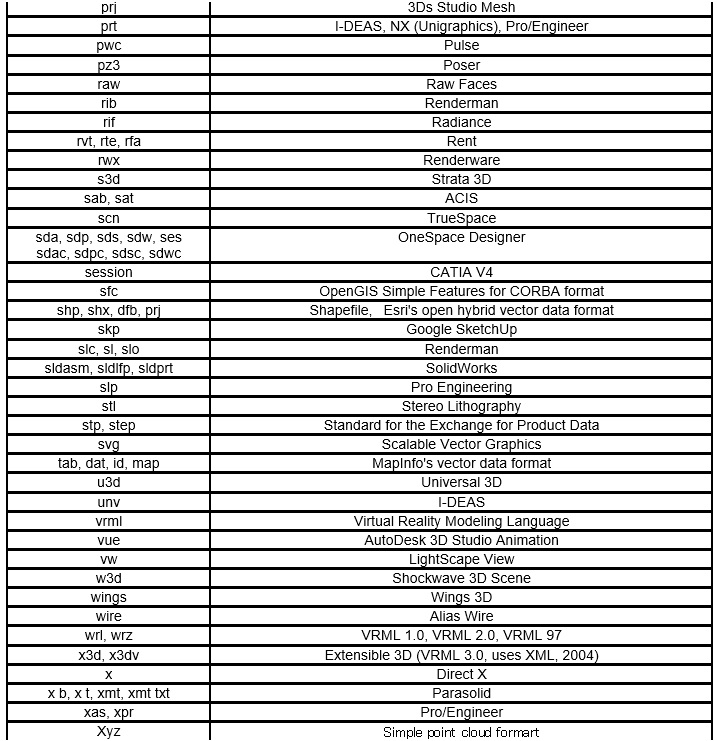
2010年調査（拡張子、定義書、サンプルデータと表示画像）

最近(2010-20)では、
Googleの無償三次元モデラー(sketch up)と、GoogleEarth と重ね表示ができるKML,KMZ形式が普及したが、その後も新たなデータ形式が増加中
三次元プリンタにSTL形式によるソリッドモデルの三次元データが広く用いられている
レーザースキャナで計測した点群データ（PCLOUD）も普及している

実践

７．建設省→国土交通省における標準化
８．標準化のもつジレンマとメタファイル方式への提案
９．IFC形式を題材としたいくつかの試み（2014-)

７．建設省→国土交通省における標準化

・建築確認申請（BASIC、90年代、三次元）
FD申請の一方法として施行細則で定義されたが殆ど実行されず、廃止
BS変換結果
・道路（SCADEC→LandXML）二次元
（在来紙図面の平面図、横断図、縦断図を記述する。頂点の対応が明確になることにより、三次元化が容易。
SCADECでは二次元ベクトルデータ、LandXMLでは頂点のIDにより自動マッチングが可能）

(前略）
<CgPoints name="ElementPnts">
<CgPoint name="BP">23734.911081433722 314232.62649047165</CgPoint>
<CgPoint name="KA-1">23730.425888305144 314257.51480917312</CgPoint>
<CgPoint name="BC-1">23719.523924020039 314306.27623879386</CgPoint>
<CgPoint name="EC-1">23678.088311166004 314379.46691226994</CgPoint>
<CgPoint name="KE-1">23641.887767692468 314413.90599611594</CgPoint>
<CgPoint name="KA-2">23625.126485068737 314428.57141764683</CgPoint>
<CgPoint name="BC-2">23588.925941595193 314463.01050149283</CgPoint>
<CgPoint name="EC-2">23552.562164813575 314521.91787131043</CgPoint>
<CgPoint name="KE-2">23537.998763615044 314569.71365762537</CgPoint>
<CgPoint name="EP">23527.37604411077 314610.61487586098</CgPoint>
</CgPoints>
<Alignments name="○○路線">
<Alignment name="線形_1" length="444.134495064822" staStart="0.">
<CoordGeom>
<Line length="25.289234175568">
<Start pntRef="BP"/>
<End pntRef="KA-1"/>
</Line>
<Spiral length="50." radiusEnd="200." radiusStart="INF" rot="cw" spiType="clothoid">
<Start pntRef="KA-1"/>
<PI>23724.509181464713 314290.34659172664</PI>
<End pntRef="BC-1"/>
</Spiral>
<Curve rot="cw" radius="200.">
<Start pntRef="BC-1"/>
<Center>23528.652651826989 314246.54218274995</Center>
<End pntRef="EC-1"/>
</Curve>
<Spiral length="50." radiusEnd="INF" radiusStart="200." rot="cw" spiType="clothoid">
<Start pntRef="EC-1"/>
<PI>23666.994740072652 314391.93844496924</PI>
<End pntRef="KE-1"/>
</Spiral>
(後略）

LandXML

　建築確認(BASIC)では、建築図面の「文化」を無視して一挙に三次元化を図り、普及しなかった。図面から手入力で三次元データが作成されている。
　土木電子納品では、紙時代の「平面図」「横断図」「縦断図」をそのままコーディングしようとしている。二次元データであるが、自動認識による立体生成はかなり容易になった。
　建築分野では厖大に蓄積されている紙図面と二次元CADデータの自動立体認識が生産性向上の課題と考える。

・地形データ：標高モデル（MEM、LEM）
ステレオ空中写真自動解析により作成したMEM
航空機搭載レーザースキャナにより計測したLEM
首都圏・大都市圏で先行的に整備されていたが、
2011.3.11東日本大震災後、津波被災地沿岸で計測された。
・基盤地図情報（標高、xml形式）
・電子国土

８．標準化のもつジレンマと
メタファイル方式への提案

・同時代的共有のためには標準化された方が便利
・将来技術の展開は標準からの逸脱を必要とする

・拡張子やヘッダーによる定義ではなく、
「完全なメタファイル」（解読プログラム）を添付
・解読プログラムの記述方法を再現可能とする
（再読可能な過去の記録として封印する）

９．IFC形式を題材とした
いくつかの試み（2014-)

(1)記録データ作成(2014)
(2)景観シミュレータ外部関数 IFC.exe による変換 (2014、今回改良2019.8-9)
(3)データ毎のメタファイル IFC.cmmによる変換(2015-8)
(4)WebGLによる入力・表示

(1)記録データ作成(2014)

・旧建設省建築研究所：新宿百人町庁舎の記録図面の発見(2014)
保存のためにCAD入力作成したIFC形式データ
（入力における欠陥と、処理系による「方言」問題）

#21=IFCBUILDINGELEMENTPROXY('^tc04>U@|whP&J-hW$C;',$,'\X\89\X\AE\X\8D\X\AA\X\00\X\AA',$,$,#22,#25,$,$);
#22=IFCLOCALPLACEMENT(#15842,#23);
#23=IFCAXIS2PLACEMENT3D(#24,$,$);
#24=IFCCARTESIANPOINT((0.0,0.0,0.0));
#25=IFCPRODUCTREPRESENTATION($,$,(#26));
#26=IFCSHAPEREPRESENTATION($,'Body','SurfaceModel',(#27));
#27=IFCFACEBASEDSURFACEMODEL((#30));
#28=IFCAXIS2PLACEMENT3D(#29,$,$);
#29=IFCCARTESIANPOINT((0.0,0.0,0.0));
#30=IFCCONNECTEDFACESET((#405,#409,#413,#417,#423,#429,#433,#439,#443,#447,#451,
#455,#459,#463,#467,#470,#473,#477,#480,#483,#486,#489,#492,#496,#499,#502,#506,
#510,#515,#518,#521,#524,#528,#531,#537,#541,#544,#547,#550,#553,#556,#559,#31,
#63,#42,#37,#76,#60,#55,#49,#67,#70,#79,#45,#73,#612,#615,#621,#625,#629,#633,
#637,#641,#644,#647,#650,#653,#656,#659,#82,#85,#88,#91,#94,#97,#100,#103,#109,
#113,#119,#123,#126,#129,#239,#244,#248,#251,#257,#261,#265,#269,#275,#279,#285,
#289,#295,#299,#132,#135,#138,#141,#144,#147,#153,#157,#161,#165,#169,#172,#176,
#179,#303,#307,#311,#315,#320,#323,#326,#329,#332,#335,#339,#342,#346,#349,#182,
#185,#191,#195,#199,#203,#207,#211,#216,#219,#223,#227,#230,#233,#662,#665,#668,
#671,#674,#677,#680,#683,#689,#693,#699,#703,#707,#711,#715,#719,#722,#725,#731,
#735,#740,#743,#748,#751,#754,#562,#565,#568,#571,#574,#577,#580,#583,#586,#589,
#595,#599,#604,#607,#352,#355,#359,#363,#367,#370,#373,#376,#380,#383,#386,#389,
#395,#399));
#31=IFCFACE((#32));
#32=IFCFACEOUTERBOUND(#33,.T.);
#33=IFCPOLYLOOP((#34,#35,#36));
#34=IFCCARTESIANPOINT((2146.669921875,5846.669921875,8764.830070437922));
#35=IFCCARTESIANPOINT((2146.669921875,5446.669921875,8624.830070437922));
#36=IFCCARTESIANPOINT((2146.669921875,5446.669921875,8898.509757937922));
#37=IFCFACE((#38));
#38=IFCFACEOUTERBOUND(#39,.T.);
#39=IFCPOLYLOOP((#40,#41,#34));
#40=IFCCARTESIANPOINT((2146.669921875,5846.669921875,9038.509757937922));
#41=IFCCARTESIANPOINT((2146.669921875,6246.669921875,8897.160148562922));
(後略）
サンプル土地 サンプル建物

(2)外部関数 IFC.exeによる変換(2014)

・景観シミュレータの外部関数 IFC.exe による解読
2014年、百人町データの納品検査用に作成
その際にBOOL演算を含むサンプルデータを使用
（revit使用）
今回(2019.8)、ArchiCADサンプルデータで増強
（方言への対応）
・IFC.exeは、将来的には特定のデータ専用ではなく、様々なデータの変換・入力・検査用として、IFCの様々なコマンドに対応する方向で増補
・実行環境はWindowsに限定

（基本形式） #番号＝IFCコマンド（引数,引数,・・・　）;
　引数は、単独の場合と、（配列）の場合がある。省略形は、「$」
（階層構造）
　最下層のデータからボトムアップで形状定義等を行う。
　IFCCARTESIANPOINT(座標値)→IFCPOLYLOOP(ループ)→IFCFACEOUTERBOUND（外周）, IFCFACEBOUND（穴）
　→IFCFACE（面）→IFCCONNECTEDFACESET(面リスト）→IFCFACEBASEDSURFACEMODEL（多面体）
　→IFCSHAPEREPRESENTATION（形状の種類と#形状データ）→IFCPRODUCTREPRESENTATION（部材の表現）
　→IFCBUILDINGELEMENTPROXY（部材のID、和文名称、配置、部材の表現）

部材の表現は、この他に、押し出し図形（断面形＋移動ベクトル）、図形演算等で表現
#616= IFCSHAPEREPRESENTATION(#88,'Body','SweptSolid',(#606));

#1726= IFCSHAPEREPRESENTATION(#88,'Body','Clipping',(#1716));
IFC.exeでは、図形演算（BOOLEAN）は、変換結果の記述において、
　Gnnn.geo=OUTPUT(Gnnn);
　Gmmm.geo=OUTPUT(Gmmm);
　DELETE(Gnnn);
　DELETE(Gmmm);
　Gnew=FILE(BOOL,Gmmm.geo,Gnnn.geo);
のコマンド群に変換している。
変換結果（LSSG形式ファイル）を読み込む段階で、演算対象を小さなファイルに出力し、
プロセスとして起動したBOOL.EXEが図形演算処理を実行してファイルとして結果を返す。
床板などにおいて、多数の部分欠き込み処理が行われている例がある。
床板BOOL  
　配置は、IFCLOCALPLACEMENT により、移動・回転を表現する
　IFCLOCALPLACEMENTは、上位の座標系に対する相対的な移動・回転として階層的に構成 　（例えば、敷地全体→建物→階→部材）
（データないしデータを出力したアプリの欠陥を検査する方法として有効）
上記の記録データは、ArchiCADのIFCファイル入力に失敗する（エラーメッセージなく、何も表示されない）
一方、ArchiCADから出力されたIFCファイルでは、以下のようになっている。
#68= IFCCARTESIANPOINT((19054.9999998,7150.00001716,300.));
#70= IFCCARTESIANPOINT((18125.,8650.,300.));
#72= IFCCARTESIANPOINT((18125.,6199.97975185,300.));
#74= IFCPOLYLOOP((#68,#70,#72));
#76= IFCFACEOUTERBOUND(#74,.T.);
#77= IFCFACE((#76));
　・・・・
#128= IFCOPENSHELL((#77,#84,#91,#98,#105,#112,#119,#126));
#130= IFCSHELLBASEDSURFACEMODEL((#128));
　・・・・
#2174= IFCSHAPEREPRESENTATION(#66,'Body','SurfaceModel',(#130,#189,#247,#299,#351,#403,#455,#507,#559,#629,#667,#720,#863,#993,#1069,#1127,#1179,
#1231,#1381,#1426,#1509,#1588,#1664,#1716,#1774,#1826,#1851,#1910,#1962,#2014,#2066,#2118,#2170));
#2181= IFCPRESENTATIONLAYERASSIGNMENT('\X2\657757305916\X0\_\X2\573076E4\X0\.\X2\2605\X0\',$,(#2174),$);
#2184= IFCPRODUCTDEFINITIONSHAPE($,$,(#2174));
#2189= IFCSITE('20FpTZCqJy2vhVJYtjuIce',#12,'\X2\30B530A430C8\X0\',$,$,#63,#2184,$,.ELEMENT.,(35,42,0,0),(139,46,0,0),0.,$,#52);
(階層構造の経路が異なっている）
IFCCATESIANPOINT→IFCPOLYLOOP→IFCFACEOUTERBOUND→
IFCFACE→IFCOPENSHELL→IFCSHELLBASEDSURFACEMODEL→IFCSHAPEREPRESENTATION
(二つの階層構造をサポートすることにより、どちらも入力できるコンバータとなる）

図形演算の改良
半無限刃物 
穴あき平面の表現
スピーカーの穴
IFCFACEコマンドで、
１のIFCFACEOUTERBOUND（外周）と、
複数のIFCFACEBOUND（穴）を指定

　　巻いた図形（手摺の端面に多発）
　　データの欠陥に起因して、エラーメッセージが多数発生
手摺の端面
　　　　原因はデータ入力を行った処理系。
　　　　OpenGL表示における⊿分割段階で発覚。

#1131519= IFCFACE((#1130226,#1130253,#1130280,#1130307,#1130334,#1130361,#1130388
,#1130415,#1130442,#1130469,#1130496,#1130523,#1130550,#1130577,#1130604,#1130631
,#1130658,#1130685,#1130712,#1130739,#1130766,#1130793,#1130820,#1130847,#1130874
,#1130901,#1130928,#1130955,#1130982,#1131009,#1131036,#1131063,#1131090,#1131117
,#1131144,#1131171,#1131198,#1131225,#1131252,#1131279,#1131306,#1131333,#1131360
,#1131387,#1131414,#1131441,#1131468,#1131491,#1131518));
→その後の進展と残された課題

(3)データ毎のメタファイルによる変換(2015-8)

・個別ファイル解読用IFC.cmmのチューンナップ
データ毎の十分な固定長配列を使用
データファイル中に使用されていないコマンドの解析を省略
当該データファイルに固有の欠陥個所のスキップ・修正
(通常何らかの欠陥のあるオリジナルデータの原本自体は修正しない。）
メタファイルの実行環境（2019.9時点）：
(1)PC上で、景観シミュレータから起動する
(1-1)形状生成オプションから起動する外部関数 VC-1C
(1-2)プラグインdll VC-2V
(2)PC上でスタンドアロン起動する実行形式
(2-1)VC-1c.exe
(2-2)VC-4d.exe
(3)AndroidタブレットでAR表示する
VC-3M.apk(通常は、特定の記録データにバインドして配布）

（cmmの解析例）
int cartesianpoint1(int nl){
　int pos,i;
　int rc,ip,iv;
　quat q;
　pos = SIORI();
　SEEK(LineCounter[nl]);
　rc = scanf("CARTESIANPOINT((%qx,%qy,%qz)",q);
　q *= QUNIT;
　if(rc != 3) ERROR(nl,rc,SIORI());
　skip();
　SEEK(pos);
　return COORD(q);
}

int polyloop1(int nl){
　int pos,i,p0,p1,p2,rc;
　pos = SIORI();
　rc = 0;
　SEEK(LineCounter[nl]);
　if(!scanf("POLYLOOP(")){
　 logf("#NOT POLYLOOP COMMAND\n");
　 thru();
　}else{
　//　logf("#%03d=POLYLOOP1 COMMAND\n",nl);
　　　rc = scanf("(#%d",p0);
　　　rc += scanf(",#%d",p1);
　　　rc += scanf(",#%d)",p2);
　　　if(rc != 3){
　　　　logf("#POLYLOOP FORMAT ERROR\n");
　　　　rc = 0;
　　　}else if(p0==p1){
　　　　logf("#POLYLOOP ERROR(p0==p1)\n");
　　　　rc = 0;
　　　}else if(p1==p2){
　　　　logf("#POLYLOOP ERROR(p1==p1)\n");
　　　　rc = 0;
　　　}else if(p2==p0){
　　　　logf("#POLYLOOP ERROR(p2==p0)\n");
　　　　rc = 0;
　　　}else{
　P0 = cartesianpoint1(p0);
　P1 = cartesianpoint1(p1);
　P2 = cartesianpoint1(p2);
　rc = 1;
　}
　}
　SEEK(pos);
　return rc;
}

百人町建物（本館正面壁）のデータに
見られる異常の例とその修正
本館正面⊿分割
壁面の三角形分割状況
表裏逆転
表裏が逆転している部分
表裏修正
修正後(表示確認ではわからない面の表裏は、
例えば図形演算や三次元プリンタ出力で重要となる）

(4)WebGLによる入力・表示(2019)

・JavaScript用いたファイル解析処理と、WebGLによる表示 （HTML canvas 要素の中に描画を行う）

正規表現による構文解析などの試作例
/（コマンド）/.文字列（１行分）でコマンドを検出
連想配列 pointdic, loopdic, facedic 等に、コマンドが存在する行番号を登録
　　reader.addEventListener( 'load', function() {
　　　　ifcs = reader.result.split('\n');
　　　　nifc = ifcs.length;
　　　　resetdic();
　　　　for(i=0; i<nifc; i++){
　　　　　if( /IFCCARTESIANPOINT/.test(ifcs[i]) ) pointdic[ifcs[i].match(/#\d+/)[0]]=i;
　　　　　else if( /IFCPOLYLOOP/.test(ifcs[i]) ) loopdic[ifcs[i].match(/#\d+/)[0]]=i;
　　　　　else if( /IFCFACE\(/.test(ifcs[i]) ) facedic[ifcs[i].match(/#\d+/)[0]]=i;
　　　　　else if( /IFCFACEOUTERBOUND/.test(ifcs[i]) )
　　　　　　bounddic[ifcs[i].match(/#\d+/)[0]]=i;
　　　　　else if( /IFCFACEBOUND/.test(ifcs[i]) ) bounddic[ifcs[i].match(/#\d+/)[0]]=i;
　　　　　else if( /IFCCONNECTEDFACESET/.test(ifcs[i]) )
　　　　　　gfacedic[ifcs[i].match(/#\d+/)[0]]=i;
　　　　　else if( /IFCCLOSEDSHELL/.test(ifcs[i]) ) gfacedic[ifcs[i].match(/#\d+/)[0]]=i;
　　　　}
・・・・・・・（後略）

小結：
(1)WebGLを用いることにより、クライアント側の計算パワー(PC、スマホ、タブレット）で表示が可能。
(2)Three.js ライブラリを使用することにより、ジオメトリの入力処理（プログラミング）省力可能。
(3)穴あき図形と三次元BOOL演算を行うライブラリがあれば、多様なIFC形式を処理可能。